Zero Power Property of Exponents
Property —
Zero Power Property
English Any real number, except zero, raised to the power 0 is 1.
Algebra x0 = 1, x ≠0
Example 170 = 1
Here’s a way to understand why 170 is 1.
Suppose we write 0 as 2 - 2. Then, 170 = 172 - 2.
By the Division Property of Exponents,
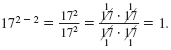 Since
170 = 172 - 2 and 172 - 2 = 1, we have 170
= 1.
Note:
This same reasoning applies no matter
what power or nonzero base we choose.
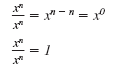
Therefore, x0 = 1 for x ≠ 0.
Example 1
a. Use the Zero Power Property to simplify 50.
b. Justify your answer.
Solution
| a. Any real number, except zero,
raised to the power 0 is 1.
|
50 = 1 |
|
b. Suppose we have
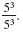
We can simplify this using the
Division Property of Exponents.
But if we reduce the fraction
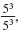 the result is 1. the result is 1.
Since
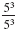 is equivalent to both 50 and 1,
we conclude 50 = 1. is equivalent to both 50 and 1,
we conclude 50 = 1. |
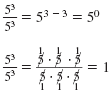 |
Example 2
Find each of the following. (Assume each variable represents a nonzero
real number).
| a. (-7)0 |
b.
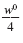 |
c. (12x4y5)0 |
d. -2y0 |
e. 00 |
Solution
In each case, we apply the Zero Power Property: any nonzero real number
raised to the zero power is 1.
| a. The base is the real number -7. |
(-7)0 |
= 1 |
| b. The base, w, represents a nonzero real number. |
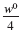 |
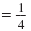 |
| c. The base, 12x4y5, represents a nonzero
real number. |
(12x4y5)0 |
= 1 |
| d. Only y is raised to the power 0. |
-2y0 = -2
· 1 |
= -2 |
| e. In the Zero Power Property,
the base cannot be 0. |
00 is undefined |
|