Completing the Square
The essential part of completing the square is to recognize a perfect square trinomial
when given its first two terms. For example, if we are given x2 + 6x, how do we recognize that these are the first two terms of the perfect square trinomial
x2 + 6x + 9? To answer this question, recall that
x2 + 6x + 9 is a perfect square
trinomial because it is the square of the binomial x + 3:
(x + 3)2 = x2 + 2 · 3x + 32 = x2
+ 6x + 9
Notice that the 6 comes frommultiplying 3 by 2 and the 9 comes from squaring the 3.
So to find the missing 9 in x2 + 6x, divide 6 by 2 to get 3, then square 3 to get 9. This
procedure can be used to find the last term in any perfect square trinomial in which
the coefficient of x2 is 1.
Rule for Finding the Last Term
The last term of a perfect square trinomial is the square of one-half of the
coefficient of the middle term. In symbols, the perfect square trinomial whose
first two terms are
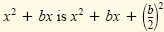 . .
Helpful hint
Review the rule for squaring a
binomial: square the first term,
find twice the product of the
two terms, then square the
last term. If you are still using
FOIL to find the square of a binomial,
it is time to learn the
proper rule.
Example 1
Finding the last term
Find the perfect square trinomial whose first two terms are given.

Solution
a) One-half of 8 is 4, and 4 squared is 16. So the perfect square trinomial is
x2 + 8x + 16.
b) One-half of -5 is
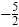 , and , and
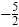 squared is squared is
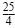 . So the perfect square trinomial is . So the perfect square trinomial is
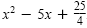 . .
c) One-half of
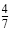 is is
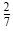 , and , and
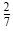 squared is squared is
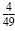 . So the perfect square trinomial is . So the perfect square trinomial is
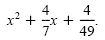
d) One-half of
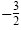 is is
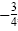 , and , and
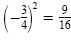 . So the perfect square trinomial is . So the perfect square trinomial is
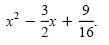
Another essential step in completing the square is to write the perfect square
trinomial as the square of a binomial. Recall that
a2 + 2ab + b2 = (a + b)2 and
a2 - 2ab + b2 = (a - b)2.
Example 2
Factoring perfect square trinomials
Factor each trinomial.
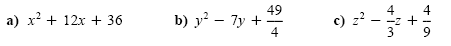
Solution
a) The trinomial x2 + 12x + 36 is of the form a2 + 2ab
+ b2 with a = x and
b = 6. So
x2 + 12x + 36 = (x + 6)2.
Check by squaring x + 6.
b) The trinomial
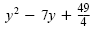 is of the form a2
- 2ab + b2 with a
=
y and is of the form a2
- 2ab + b2 with a
=
y and
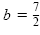 . So . So
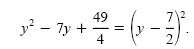
Check by squaring
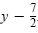 . .
c) The trinomial
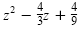 is of the form a2
- 2ab + b2 with a = z and is of the form a2
- 2ab + b2 with a = z and
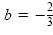 . So . So
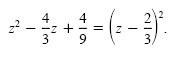
|