Finding the Least Common Multiples
The multiples of a number are the products of that number and
the whole numbers. For instance the multiples of 5 are the
following.
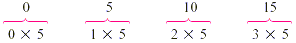
A number that is a multiple of two or more numbers is called a
common multiple of these numbers. To find the common multiples of
6 and 8, we first list the multiples of 6 and the multiples of 8
separately.
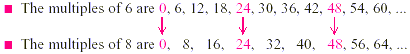
So the common multiples of 6 and 8 are 0, 24, 48, ... . Of the
nonzero common multiples, the least common multiple of 6 and 8 is
24.
Definition
The least common multiple (LCM) of two or
more numbers is the smallest nonzero number that is a multiple of
each number.
A shortcut for finding the LCM—faster than listing
multiples—involves prime factorization.
To Compute the Least Common Multiple (LCM)
- find the prime factorization of each number,
- identify the prime factors that appear in each
factorization, and
- multiply these prime factors, using each factor the
greatest number of times that itoccurs in any of the
factorizations.
EXAMPLE 1
Find the LCM of 8 and 12.
Solution
We first find the prime factorization of each number.
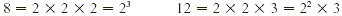
The factor 2 appears three times in the factorization of 8 and
twice in the factorization of 12, so it must be included three
times in forming the least common multiple.

As always, it is a good idea to check that our answer makes
sense. We do so by verifying that 8 and 12 really are factors of
24.
EXAMPLE 2
Find the LCM of 5 and 9.
Solution
First we write each number as the product of primes.
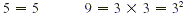
To find the LCM we multiply the highest power of each prime.
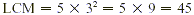
So the LCM of 5 and 9 is 45. Note that 45 is also the product
of 5 and 9. Checking our answer, we see that 45 is a multiple of
both 5 and 9.
TIP
If two or more numbers have no common factor (other than 1),
the LCM is their product.
Now let's find the LCM of three numbers.
EXAMPLE 3
Find the LCM of 3, 5, and 6.
Solution
First we find the prime factorizations of these three numbers.
3 = 3
5 = 5
6 = 2 × 3
The LCM is therefore the product 2 × 3 × 5, which is 30.
Note that 30 is a multiple of 3, 5, and 6, which supports our
answer.
EXAMPLE 4
A gym that is open every day of the week offers aerobic
classes everythird day and gymnastic classes every fourth day.
You took both classesthis morning. In how many days will the gym
offer both classes on thesame day?
Solution
To answer this question, we ask: What is the LCM of 3 and 4?
As usual, we begin by finding prime factorizations.
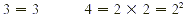
To find the LCM, we multiply 3 by 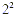 . .
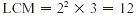
Both classes will be offered again on the same day in 12 days.
|