Slope
Objective Learn the concept of the slope of a
line and to evaluate it for particular lines.
In this lesson, you will be introduced to the notion of the
slope of a straight line. It is very important that you see many
examples, and that you do many exercises by yourself. In these
exercises, you should use the formula for slope so that you
become familiar with using it. You should also write and solve
your own exercises involving slope. It is desirable that you have
grid paper for this lesson.
Slope
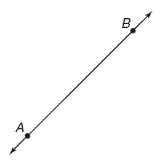
First, let's talk in intuitive terms about what is meant by
slope. We can assign a number that allows us to measure the
steepness of a straight line. Also, the greater the absolute
value of this number, the steeper the line will be. If you draw a
straight line with two points on it, A and B, there are two
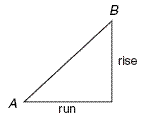
numbers attached to this pair of points, namely the rise and the
run . The rise is how much higher B is than A in the vertical
direction, and the run is how far over from A point B is in the
horizontal direction.
Definition of Slope
Words The slope is the value of the quotient  .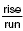
Model
So far, we have talked about lines without placing them in the
coordinate plane. Let's try to understand slope better by
studying lines in the coordinate plane. Start by plotting the
sequence of points (1, 1), (2, 2), (3, 3), and (4, 4) and try to
find out what the pattern is. Find the value of y in ( -1, y ).
Next, plot (1, 2), (2, 4), (3, 6), and (4, 8) on another
coordinate plane and try to find out what the pattern is. What do
the two sets of plotted points have in common? (Both sets of
points lie on a straight line.)
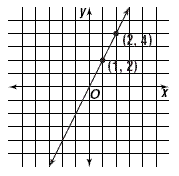
The two points plotted at the figure above have coordinates
(1, 2) and (2, 4). The rise is the difference between 4 and 2, so
it equals 2. The run is the difference between 2 and 1, so it
equals 1. The slope is the quotient 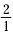 or 2. Next, we choose two different points on the
same line, say (0, 0) and (3, 6), and compute the slope again.
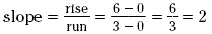
Key Idea
The slope is the same for any pair of points on the same
straight line. Therefore, it is not necessary to refer to a
particular pair of points when speaking of the slope of a line.
Note that the y-difference is the numerator and the
x-difference is the denominator.
|
