Pythagoras' theorem
Pythagoras' theorem relates the lengths of the sides of a
right-angled triangle. This leaflet reminds you of the theorem
and provides some revision examples and exercises.
Study the right-angled triangle shown.
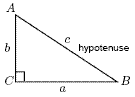
In any right-angled triangle, ABC , the side opposite the
right-angle is called the hypotenuse. Here we use the convention
that the side opposite angle A is labelled a. The side opposite B
is labelled b and the side opposite C is labelled c. Pythagoras'
theorem states that the square of the hypotenuse, (c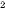 ),
is equal to the sum of the squares of the other two sides, (a ),
is equal to the sum of the squares of the other two sides, (a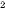 +
b +
b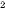 ) )
Pythagoras' theorem: c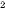 =
a =
a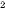 + b + b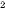
Example
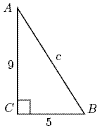
Suppose AC = 9 cm and BC = 5 cm as shown. Find the length of
the hypotenuse, AB .
Solution
Here, a = BC = 5, and b = AC = 9. Using the theorem
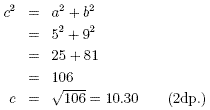
The hypotenuse has length 10.30cm.
Example
In triangle ABC shown, suppose that the length of the
hypotenuse is 14cm and that a = BC = 3 cm. Find the length of AC.
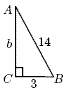
Solution
Here a = BC = 3, and c = AB = 14. Using the theorem
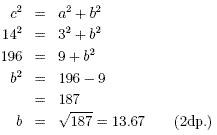
The length of AC is 13.67cm.
|