Solving Systems of Linear
Equations in Three Variables
In Maths it is many times necessary to solve systems of linear equations, such as
| x |
+ |
2y |
+ |
3z |
= |
1 |
| 2x |
+ |
5y |
+ |
2z |
= |
2 |
| x |
+ |
y |
+ |
z |
= |
3 |
There are are at least three ways to solve this set of equations: Elimination of variables,
Gaussian reduction, and Cramer’s rule. The first approach is described below.
Elimination of Variables
In the example, you first eliminate x from the second two equations, by subtracting twice the first equation from the second, and subtracting the first equation from the third. The three equations then become
| x |
+ |
2y |
+ |
3z |
= |
1 |
| |
|
y |
- |
4z |
= |
0 |
| |
|
-y |
- |
2z |
= |
2 |
Next, y is eliminated from the third equation, by adding the (new) second equation to the third, yielding
| x |
+ |
2y |
+ |
3z |
= |
1 |
| |
|
y |
- |
4z |
= |
0 |
| |
|
|
- |
6z |
= |
2 |
From the third equation, we conclude that
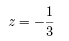
From the second equation, we conclude that
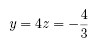
Finally, from the first equation, we find that
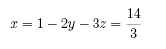
|