Multiplying Rational Expressions
Objective Learn to multiply rational
expressions.
In this lesson, you will learn to multiply rational
expressions. The techniques are completely analogous to
multiplying rational numbers (fractions). Keep this analogy in
mind throughout the entire lesson.
Multiplying Rational Numbers
Remember that to multiply rational numbers, multiply the
numerators and then divide by the product of the denominators.
Then simplify by dividing by the common factors of the numerator
and the denominator.
Example 1
Find 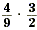 . .
Solution
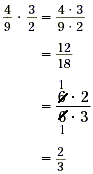 |
The GCF of the numerator and the
denominator is 6. |
| Cancel the GCF. |
An alternative way to approach this problem is to divide by
the common factors before multiplying.
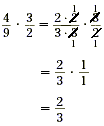
Multiplying Rational Expressions
Multiplying rational expressions is done the same way.
Multiply the numerators, and then divide the product by the
product of the denominators. Then simplify by dividing the common
factors of the numerator and the denominator.
Example 2
Find 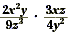 . .
Solution
Method 1:
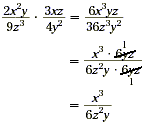 |
Cancel the GCF of the numerator and the
denominator, 6yz. |
Now just like with multiplying fractions, there is an
alternative method. Namely, divide by the common factors before
multiplying.
Method 2:
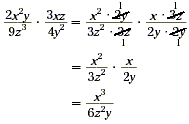
There are some problems that require factoring the polynomials
in order to find the GCF of the numerator and denominator.
Example 3
Find 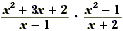 . .
Solution
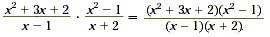
To simplify, factor the quadratic expressions in the numerator
and then cancel the common factors of the numerator and the
denominator.
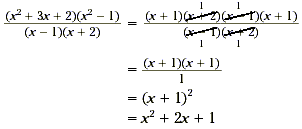
For practice, do one more example.
Example 4
Find 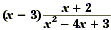 . .
Solution
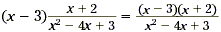
First, find the common factors. To do this, factor the
quadratic expression in the denominator.
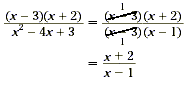 |
Cancel the common factors. |
We therefore conclude that
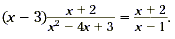
This technique is very important because it reinforces prior
techniques like factoring and multiplication of rational numbers.
|